Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики
Условия к задачам из раздела 2: "Теория вероятностей и математическая статистика" задачника: В.Ф. Чудесенко Сборник заданий по специальным курсам высшей математики (типовые расчеты). — М: Высшая школа, 1983 (1994, 2005-2009)
II. Теория вероятностей и математическая статистика: условия задачи 10
Задача 10.
Два игрока А и В поочередно бросают монету. Выигравшим считается тот, у кого раньше выпадает герб. Первый бросок делает игрок А, второй – В, третий – А и т. д.
1. Найти вероятность указанного ниже события.
Варианты 1–8. Выиграл А до k-го броска.
Варианты 9–15. Выиграл А не позднее k-го броска.
Варианты 16–23. Выиграл В до k-го броска.
Варианты 24–31. Выиграл В не позднее k-го броска.
2. Каковы вероятности выигрыша для каждого игрока при сколь угодно длительной игре?
10.1. 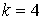 | 10.2. 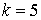 |
10.3. 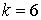 | 10.4. 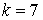 |
10.5. 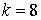 | 10.6. 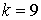 |
10.7. 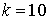 | 10.8. 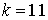 |
10.9.  | 10.10. 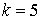 |
10.11. 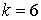 | 10.12. 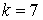 |
10.13. 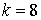 | 10.14. 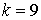 |
10.15. 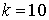 | 10.16. 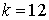 |
10.17. 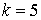 | 10.18. 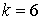 |
10.19. 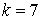 | 10.20. 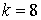 |
10.21. 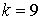 | 10.22. 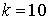 |
10.23. 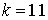 | 10.24. 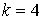 |
10.25. 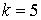 | 10.26. 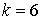 |
10.27. 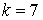 | 10.28. 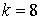 |
10.29. 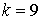 | 10.30. 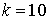 |
10.31. 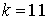 |
|
Будьте внимательны: 10 - это номер задачи, 1-31 это номер варианта.
Смотреть условия к задаче 11
| 
