Главная страница
Примеры задач
Оплата и доставка

Заказ решений

Магазин готовых решений

Учебник Кузнецова

Решения Чудесенко
   I. ТФКП и операционное исчисление
   II. Теория вероятностей и математическая статистика
      - задача 1
      - задача 2
      - задача 3
      - задача 4
      - задача 5
      - задача 6
      - задача 7
      - задача 8
      - задача 9
      - задача 10
      - задача 11
      - задача 12
      - задача 13
      - задача 14
      - задача 15
      - задача 16
      - задача 17
      - задача 18
      - задача 19
      - задача 20
      - задача 21
      - задача 22
      - задача 23
      - задача 24
      - задача 25
      - задача 26
      - задача 27
      - задача 28
      - задача 29
      - задача 30
      - задача 31
      - задача 32
      - задача 33
      - задача 34
      - задача 35
      - задача 36
      - задача 37
      - задача 38
      - задача 39
      - задача 40
      - задача 41

   III. Уравнения математической физики

Решения Берман
Задачи Рябушко
Задачи Демидович

FAQ

Ссылки

Отзывы клиентов
Решебники по другим предметам:
   Физика
   Химия
   Теоретическая механика

Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики

Условия к задачам из раздела 2: "Теория вероятностей и математическая статистика" задачника: В.Ф. Чудесенко Сборник заданий по специальным курсам высшей математики (типовые расчеты). — М: Высшая школа, 1983 (1994, 2005-2009)

Чудесенко скачать бесплатно решение задачи 29.31

Ознакомьтесь с примером решения задачи 29 вариант 31. Чтобы бесплатно скачать решение по математике (задачник Чудесенко) в хорошем качестве нажмите на рисунок.

II. Теория вероятностей и математическая статистика: условия задачи 29

Задача 29.

Вероятность наступления некоторого события в каждом из n независимых испытаний равна р. Определить вероятность того, что число m наступлений события удовлетворяет следующему неравенству.

Варианты 1–11:

;
Варианты 12–21:

;
Варианты 22–31:

29.1.	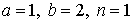29.2.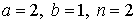
29.3.	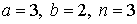29.4.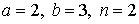
29.5.	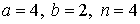29.6.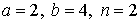
29.7.	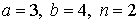29.8.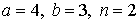
29.9.	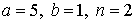29.10.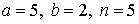
29.11.	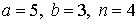29.12.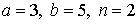
29.13.	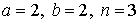29.14.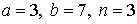
29.15.	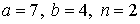29.16.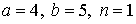
29.17.	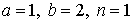29.18.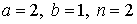
29.19.	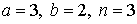29.20.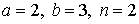
29.21.	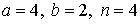29.22.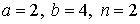
29.23.	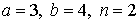29.24.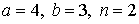
29.25.	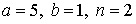29.26.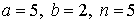
29.27.	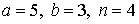29.28.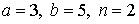
29.29.	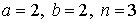29.30.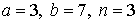
29.31.